Visualização
Medidas resumo
Os resultados de um experimento geralmente apresentam variabilidade. Esta variabilidade pode acontecer, por exemplo, por falta de controle nas condições experimentais, por erros de medição, ou pela complexidade inerente ao fenômeno observado. Assim, se obtivermos um número elevado de observações, pode ser difícil obter informações relevantes meramente olhando para o banco de dados. Por exemplo, considere o valor da causa nas primeiras 100 ações cíveis observadas em (Corrêa and Stern 2025). O que você consegue observar?
require(tidyverse)
require(readxl)
data = read_xlsx("./dados_civeis.xlsx") %>%
select(-processo_por_dependencia)
normais = data$valor_numerico
data$valor_numerico[1:100]## [1] 10673.97 86000.00 35603.04 31224.51 173425.73 33220.64
## [7] 569561.33 198940.25 277603.20 72157.76 1078863.60 553426.90
## [13] 15917.56 30000.00 43831.28 NA 15708933.66 1000.00
## [19] 30856.00 1340270.00 429332.56 NA 233193.09 328832.36
## [25] 163530.58 9420.58 27000.00 29060.04 45620.62 208476.08
## [31] 64618.88 106500.00 653273.91 1198278.30 2728.17 1000000.00
## [37] 22332.00 14050.00 138467.48 10000.00 40000.00 6140.90
## [43] 39854.97 37907.01 2100000.00 1247588.71 295714.50 18480.00
## [49] 92667.67 9500.14 100000.00 117403.78 113890.00 194243.18
## [55] 740500.00 278746.67 260000.00 175000.00 63579.16 13200.00
## [61] 20988.40 3920989.95 40.02 12631.06 13500.00 16337.32
## [67] 28196.78 28611.33 609163.45 10000.00 10000.00 31203.66
## [73] 47772.00 17916.77 10000.00 13943.70 16124.06 15000.00
## [79] 65650.33 6246.06 89922.86 84023.72 82606.00 13019.37
## [85] 75682.40 6761.58 12000.00 10000.00 10099.99 795882.49
## [91] 66469.72 10000.00 28000.00 22026.35 878377.21 15577.26
## [97] 30354.69 92000.00 10000.00 21593.81Ao invés da inspeção direta de uma variável, podemos resumí-la em valores que expressam algumas de suas características. A seguir, estudaremos algumas destas medidas de resumo.
Medidas de centralidade
Uma medida de centralidade descreve um número ao redor dos quais as observações se concentram. Ela expressa um valor ``típico’’ nas observações para uma determinada variável. Existem várias possíveis medidas de centralidade, algumas das quais veremos a seguir.
Média
A média de uma variável, comumente designada por
No R, a média pode ser calculada usando o comando mean(). Por exemplo, a média do dos valores de causa pode ser calculada da seguinte forma:
mean(data$valor_numerico, na.rm = TRUE)## [1] 315132.3Mediana
A mediana de uma variável é um número tal que há a mesma quantia de observações acima e abaixo dele. No R, a mediana é calculada pela função median().
median(data$valor_numerico, na.rm = TRUE)## [1] 16149.46A mediana é menos afetada por valores extremos do que a média. Por isso, é comum dizer que a mediana é uma medida robusta. Este conceito é ilustrado a seguir.
dados = c(0, 0.1, 0.1, 0.2, 0.25, 0.5, 0.7, 0.9, 1.1, 10000)
c(mean(dados), median(dados))## [1] 1000.385 0.375Observamos que, dos 10 dados, 9 estão concentrados próximo a 0 e 1 tem o valor 10.000. Enquanto que a média de aproximadamente 1.000 é afetada pelo valor extremo, a mediana de 0.375 não o é. É comum chamarmos observações atípicas, como o valor 10.000 neste caso, de outliers. Para o valor da causa em ações cíveis, observamos que a média é muito maior do que a mediana. Isto indica que existe um conjunto de outliers em que o valor da causa é muito maior do que no restante das ações.
Moda
A moda é o valor mais frequente observado nos dados. Como em variáveis contínuas tipicamente não observamos valores repetidos, a moda não é usado nestes casos. Por outro lado, dentre média, mediana e moda, a moda é a única medida resumo que pode ser aplicada a variáveis nominais.
No R, a função table() cria uma tabela de frequências observadas para cada valor. Aplicando esta função para a classe processual em ações cíveis, obtemos:
table(data$classe_info)##
## Carta Precatória Cível Procedimento Comum Cível
## 1 6873
## Procedimento do Juizado Especial Cível Produção Antecipada da Prova
## 9 5Assim, “Procedimento Comum Cível” é a moda da variável classe processual, sendo a categoria mais frequente neste banco de dados.
Medidas de variabilidade
Medidas de variabilidade indicam o quanto as observações variam ao redor da medida de centralidade. Em outras palavras, indicam o quão longe podemos esperar que uma observação esteja do valor típico para aquela variável. Existem diversas medidas de variabilidade, algumas das quais apresentamos a seguir.
Amplitude
A amplitude é a diferença entre o maior e o menor valor observados. Esta medida de variabilidade é fortemente influenciada por valores extremos nas observações, como outliers. O exemplo a seguir calcula a amplitude do valor da causa em ações cíveis:
max(data$valor_numerico, na.rm = TRUE) - min(data$valor_numerico, na.rm = TRUE)## [1] 681545490c(min(data$valor_numerico, na.rm = TRUE), max(data$valor_numerico, na.rm = TRUE))## [1] 10 681545500Observamos uma amplitude de quase 700 milhões. Esta amplitude pode ser causada por um único caso com valor da causa próximo a 700 milhões. De fato, apenas 3 casos tem valor superior a 100 milhões, 9 acima de 10 milhões, e 122 acima de 1 milhão:
sum(data$valor_numerico > 10^8, na.rm = TRUE)## [1] 3sum(data$valor_numerico > 10^7, na.rm = TRUE)## [1] 9sum(data$valor_numerico > 10^6, na.rm = TRUE)## [1] 122Variância e desvio padrão
Intuitivamente, podemos imaginar uma medida de variabilidade que calcule a média do quanto os dados desviam do centro. Se tomarmos como centro das observações a média, então podemos pensar no desvio da i-ésima observação como
Note que a variância não está na mesma escala das observações. Quando os desvios são elevados ao quadrado, a unidade de medida é alterada para o quadrado da unidade de medida original.
Assim, para obter uma medida mais interpretável de varibilidade, é comum tomar
a raiz quadrada da variância. Esta medida é chamada de desvio padrão,
No R a variância e o desvio padrão são calculados usando, respectivamente, as funções var() e sd(). Para o valor da causa em ações cíveis, obtemos
c(var(data$valor_numerico, na.rm = TRUE), sd(data$valor_numerico, na.rm = TRUE))## [1] 1.330321e+14 1.153395e+07Similarmente à média, a variância e o desvio padrão também são fortemente impactados por outliers. Isto explica o desvio padrão de 100 milhões encontrado no valor da causa.
Para algumas variáveis, é comum que as observações se concentrem num intervalo de 2 desvios padrão para cada lado da média. Em outras palavras, é comum que a maior parte das observações
esteja no intervalo
Amplitude interquartílica
O percentil de ordem
No R, é possível obter o percentil de ordem
aux = quantile(data$valor_numerico, c(0.25, 0.5, 0.75), na.rm = TRUE)
aux## 25% 50% 75%
## 9000.00 16149.46 41239.91Por construção, metade dos dados estão entre o
O tamanho da região em que as observações tipicamente caem é uma medida alternativa de variabilidade. Especificamente, a subtraindo o
Alternativamente, podemos construir um intervalo mais conservador exigindo que 95% das observações estejam dentro dele. Este intervalo é obtido tomando os valores entre o percentil
quantile(data$valor_numerico, c(0.025, 0.975), na.rm = TRUE)## 2.5% 97.5%
## 787.675 694093.688mean(data$valor_numerico < 5*10^5, na.rm = TRUE)## [1] 0.9663085Gráficos
Além da apresentação de medidas resumo, também é possível resumir a informação nos dados por meio de gráficos. A seguir, discutimos alguns dos principais gráficos usados.
Observação: No R, em geral existem muitas opções para gerar o mesmo gráfico. A seguir, mostraremos como gerar gráficos simples usando as funções de base do R e, também, gráficos mais elegantes, usando o pacote ggplot2. Mais informações sobre este pacote estão disponíveis aqui.
Visualizando uma variável
Strip chart
O strip chart é um gráfico para uma variável que é representado em um único eixo e é tal que, cada ponto corresponde ao valor de uma observação. Ainda que para poucas observações este gráfico possa ser informativo, quando há muitas observações ele é de difícil interpretação.
No R, o strip chart pode ser obtido pelo comando stripchart(). Para as primeiras
stripchart(data$valor_numerico[1:10], xlab="valor da causa")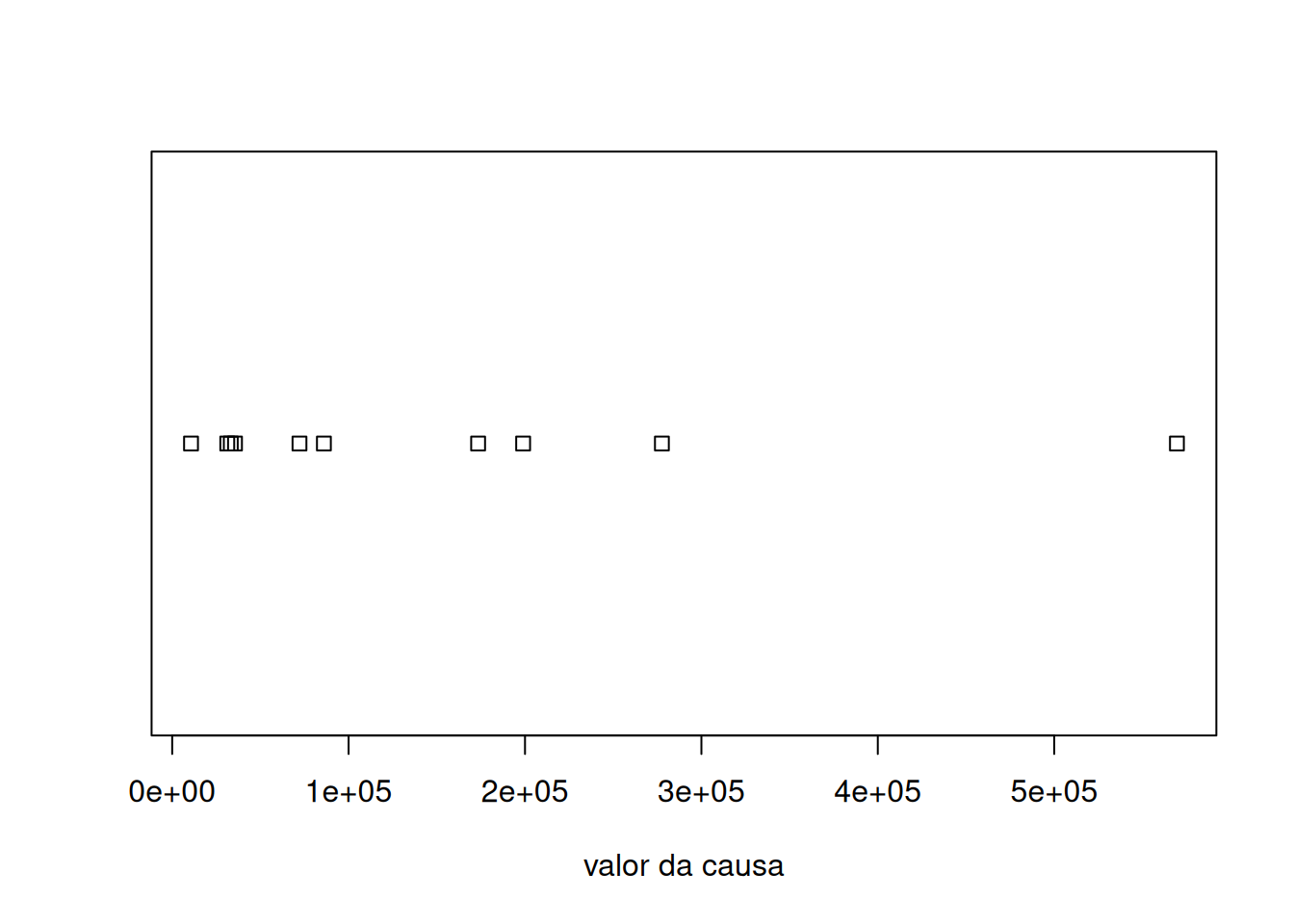
Observamos que 5 das ações tem valor da causa abaixo de 100 mil, 2 tem valor próximo a 200 mil, 1 a 300 mil, e 1 a 500 mil. O gráfico levanta uma pergunta: quais fatores diferenciam as ações com valor da causa abaixo de 100 mil daquelas com valor da causa mais alto?
A utilidade do strip chart diminui muito à medida que o tamanho da amostra aumenta. Neste caso, fica mais difícil extrair informação devido ao agrupamento dos pontos. Note como é difícil interpretar o strip chart obtido da totalidade das observações:
stripchart(data$valor_numerico, xlab="valor da causa")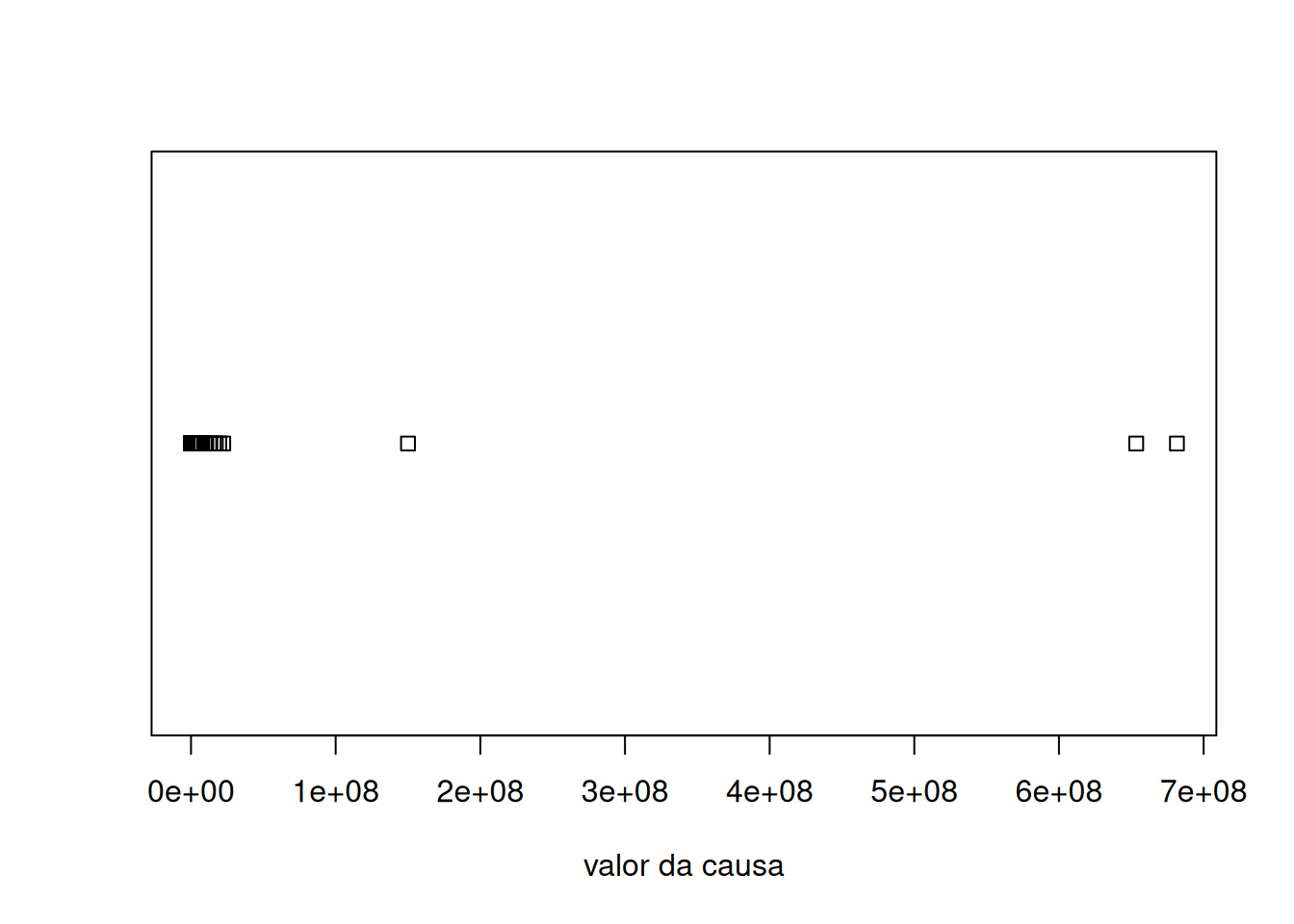
Enxergamos apenas os 3 casos em que o valor da causa é acima de 100 milhões e que há muitos casos em que o valor da causa não atinge este valor. Nestes casos, é necessário resumir as observações para obter mais informação.
Bar plot e histograma
O bar plot e o histograma são gráficos que resumem uma variável mais do que o strip chart. Ao invés de apresentarem um ponto para cada observação, estes gráficos indicam a frequência com que cada valor ocorre para uma variável.
O bar plot é usado para variáveis qualitativas e de contagem. Ele indica a contagem com que
cada valor ocorre para esta variável. Para criar um barplot no R, utilizamos primeiramente o comando table(), que conta o número de ocorrências para cada observação. A seguir, a saída do comando table é usada no comando barplot(), que exibe o gráfico. Esta sequência é ilustrada para os principais
# Colocar categorias outros
contagens = sort(table(data$assunto_info), decreasing = TRUE)[1:10]
tibble(assunto = names(contagens), contagens) %>%
ggplot(aes(x = reorder(assunto, contagens, decreasing = TRUE), y = contagens)) +
geom_bar(stat = "identity", fill = "skyblue") +
labs(title = "Gráfico de barras", x = "Assunto", y = "Contagem") +
theme(axis.text.x = element_text(angle = 20, hjust = 1))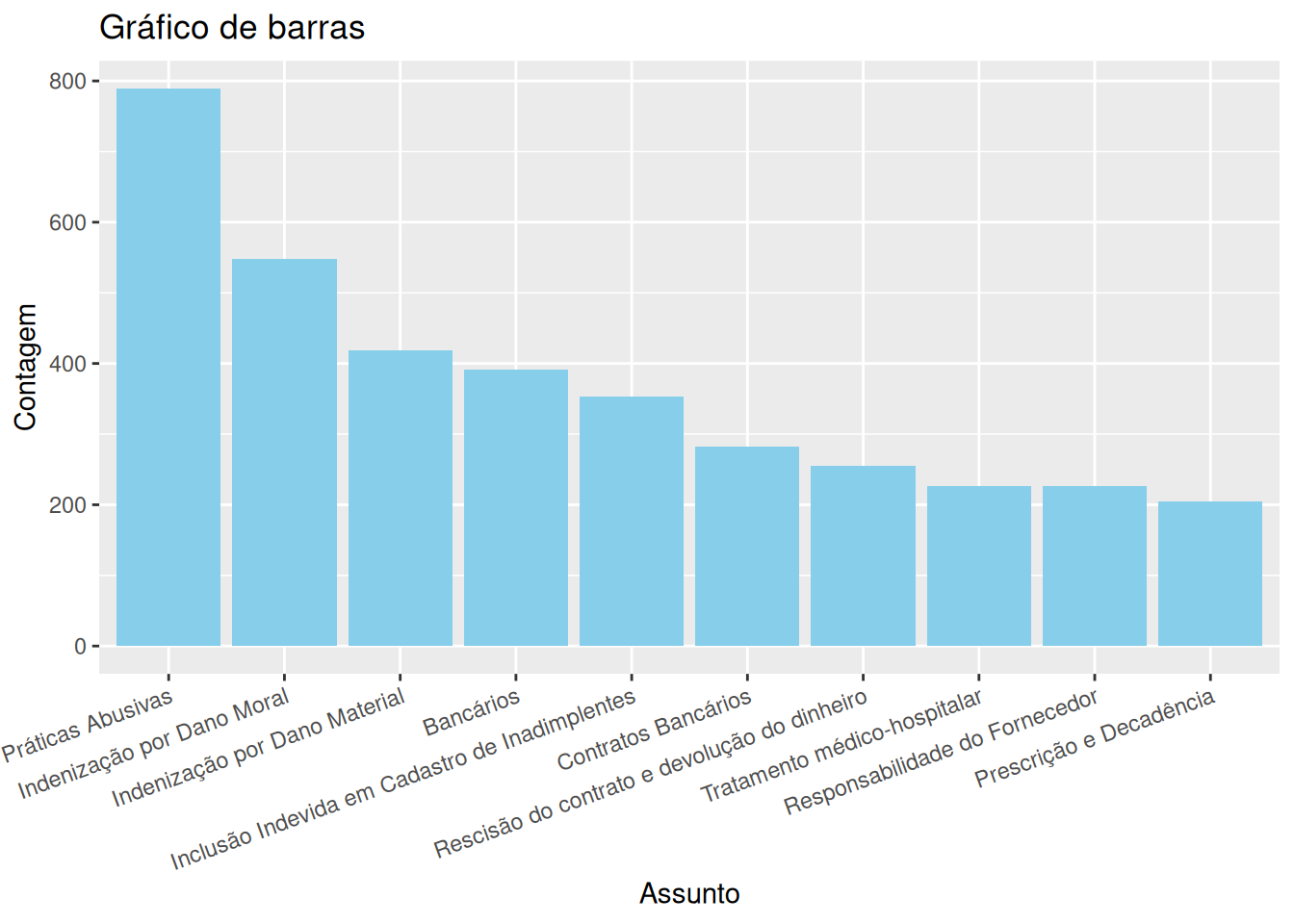
Por sua vez, o histograma é usado para variáveis quantitativas contínuas. Nestas variáveis, não esperamos encontrar duas observações que assumem o mesmo valor. Assim, o bar plot é pouco informativo. Uma alternativa é dividir os possíveis valores em faixas e contar a quantidade de observações em cada uma destas faixas. O gráfico que indica estas faixas se chama histograma. Este gráfico pode ser obtido no R pelo comando hist(). O gráfico abaixo é um histograma para o valor da causa em ações em que este valor é abaixo de 100 mil:
data %>%
filter(valor_numerico < 5*10^5) %>%
select(valor_numerico) %>%
unlist() %>%
hist(xlab="valores", ylab="contagem", main = "")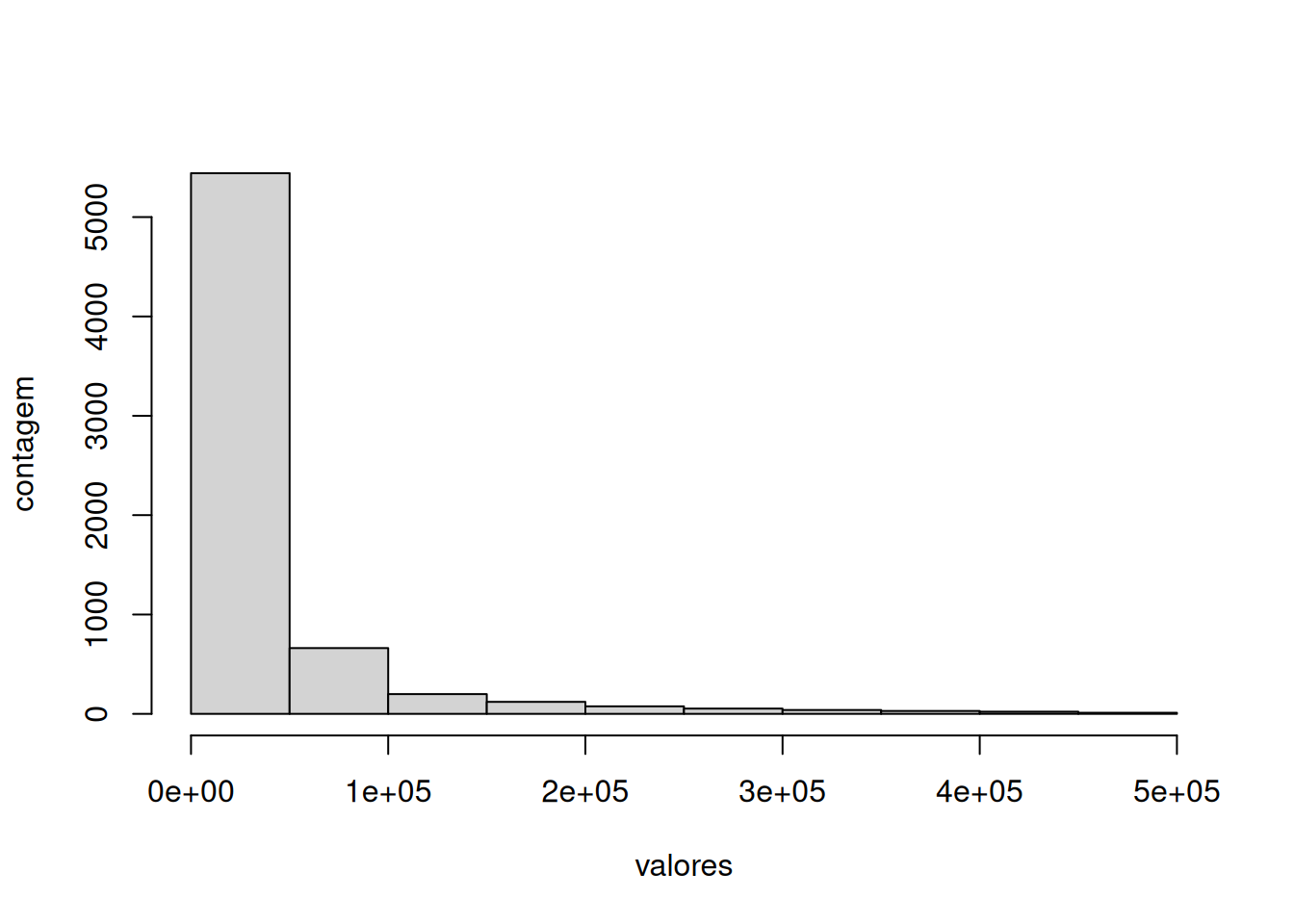
Ao contrário do strip chart, o histograma evidencia um decaimento rápido do número de casos em função do valor da causa.
Às vezes o formato de “degraus” presente no histograma pode ser indesejável. Neste caso, podemos exibir um gráfico de densidade, que cria uma curva continua em que os degraus estão ausentes. Uma das vantagens desta curva é eliminar do histograma os vãos que são gerados por faixas sem observações. A curva de densidade para o valor da causa é apresentada em vermelha e sobreposta ao histograma para estas observações na figura a seguir:
data %>%
filter(valor_numerico < 10^5) %>%
ggplot(aes(x = valor_numerico)) +
geom_histogram(aes(y=..density..)) +
geom_density(color="red") +
xlab("valor da causa") +
ylab("densidade")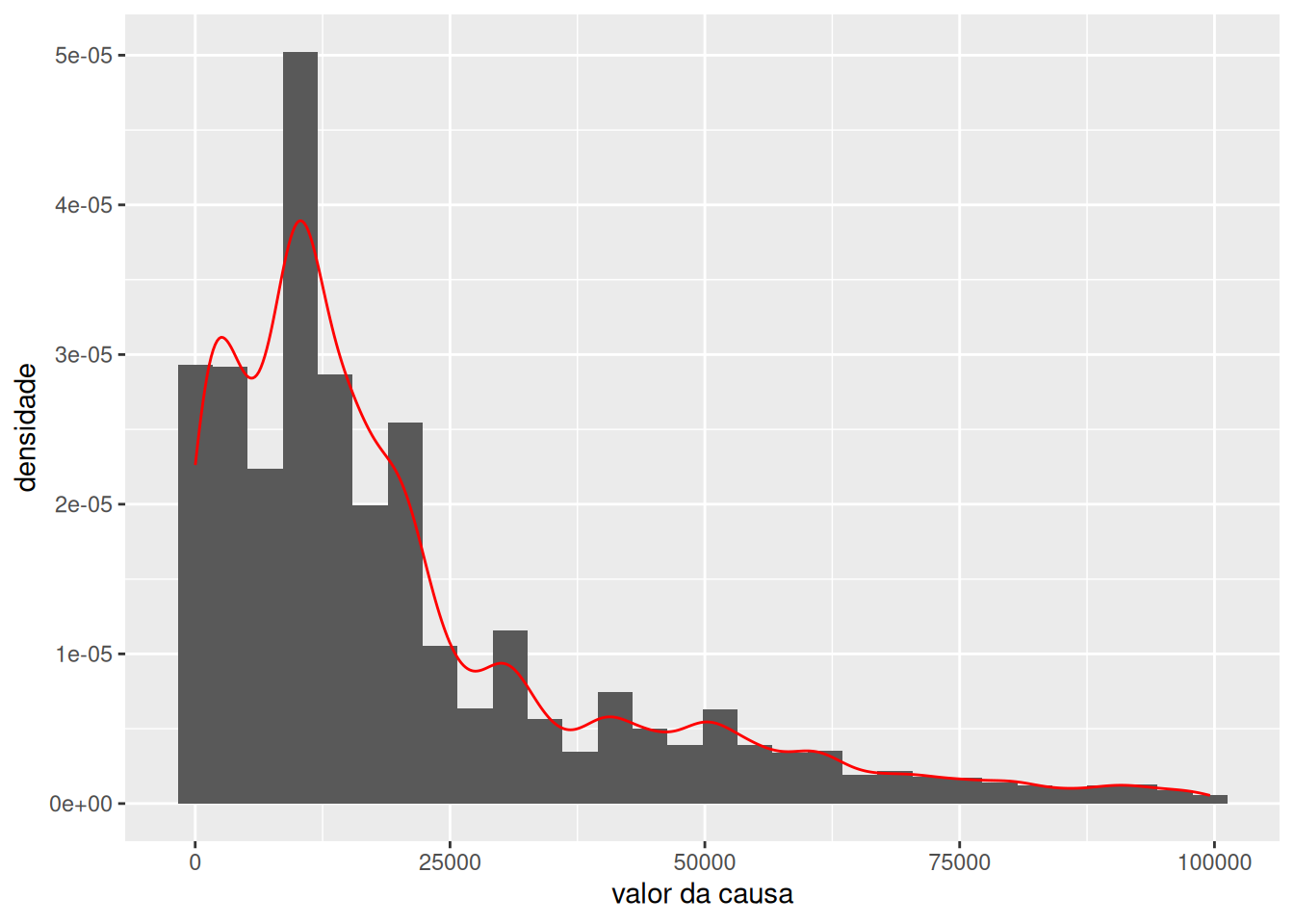
Às vezes desejamos um gráfico que resume os dados ainda mais do que um histograma. Este é o objetivo do box plot, que veremos a seguir:
Box plot
Um box plot (Tukey 1977) é um gráfico para visualizar uma única variável que consiste em apresentar visualmente 5 medidas resumo. Antes de descrever estas medidas, é útil visualizar um boxplot. No R, o box plot pode ser obtido pelo comando boxplot(). Para o valor da ação quando esta é inferior a 100 mil, obtemos:
data %>%
filter(valor_numerico < 10^5) %>%
ggplot(aes(x = valor_numerico)) +
geom_boxplot() +
xlab("Valor da causa")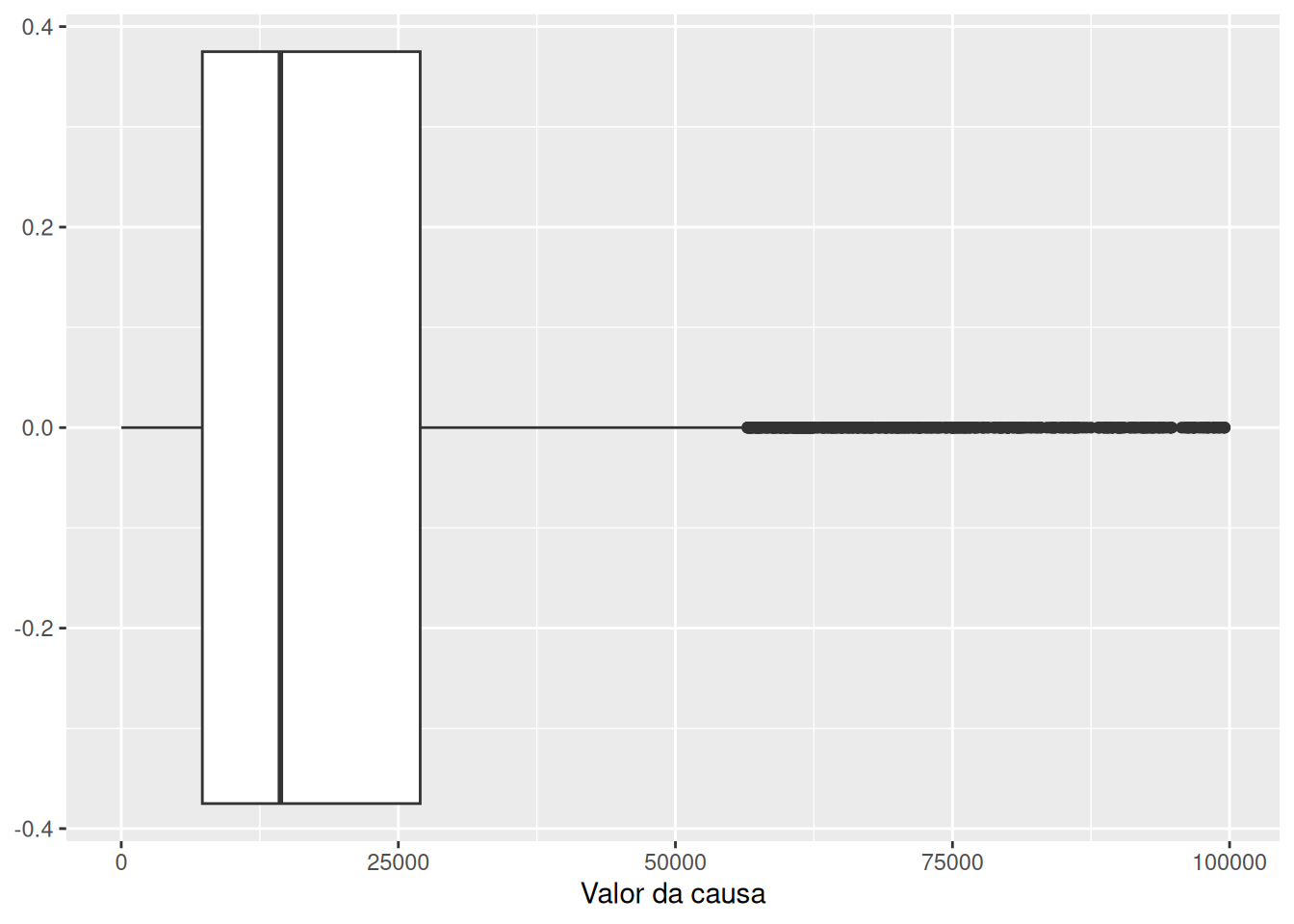
O box plot contém 5 traços principais. O traço em negrito dentro do retângulo indica a mediana (Q2) das observações. Os traços nos limites do retângulo indicam o primeiro (Q1) e o terceiro (Q3) quartis. Assim, observamos que cerca de 50% das observações estão dentro do retângulo e
que um valor típico para as observações é representado pelo traço em negrito. A seguir, lembre que a amplitude interquartílica (IQR) é definida como
Visualizando duas variáveis
Boxplot por categoria
Muitas vezes, é útil separar as observações em grupos e construir boxplots para cada um destes. O exemplo a seguir, constrói boxplots para o valor da causa quando separamos as observações por assunto.
assuntos_freq = names(sort(table(data$assunto_info), decreasing = TRUE)[1:10])
data %>%
filter(valor_numerico < 10^5) %>%
mutate(
assunto_novo = ifelse(assunto_info %in% assuntos_freq,
assunto_info,
"outros")
) %>%
ggplot(aes(y = valor_numerico, x = assunto_novo, color = assunto_novo)) +
geom_boxplot() +
theme(axis.text.x = element_blank()) +
ylab("Valor da causa")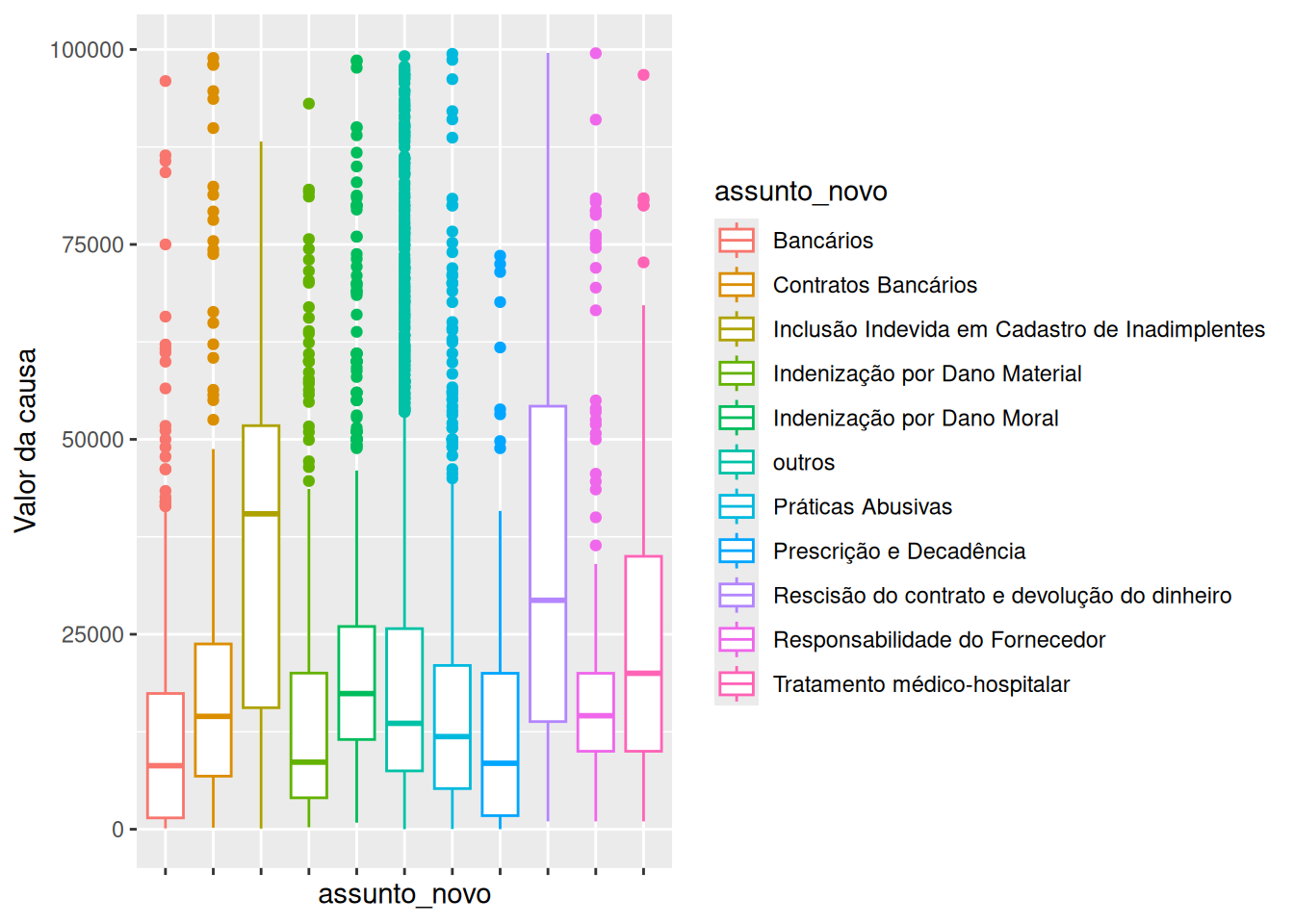 Observamos que assuntos como “inclusão indevida em cadastro de inadimplentes” e “rescisão do contrato e devolução do dinheiro” apresentam alta variabilidade, sendo que em 50% das observações o valor da causa varia de 12.500 a 50.000. Por outro lado, assuntos como “responsabilidade do fornecedor” tem variabilidade menor, com 50% das vezes o valor da causa variando entre 10.000 e 15.000.
Observamos que assuntos como “inclusão indevida em cadastro de inadimplentes” e “rescisão do contrato e devolução do dinheiro” apresentam alta variabilidade, sendo que em 50% das observações o valor da causa varia de 12.500 a 50.000. Por outro lado, assuntos como “responsabilidade do fornecedor” tem variabilidade menor, com 50% das vezes o valor da causa variando entre 10.000 e 15.000.
Scatter plot
Por vezes, estamos interessados em visualizar a relação entre duas variáveis contínuas. Neste caso, podemos designar um eixo para cada variável e desenhar um ponto para cada observação. Este tipo de gráfico é chamado de scatter plot.
No R é possível obter o scatter plot usando o comando plot().
data %>%
filter(valor_numerico < 10^5) %>%
ggplot(aes(x = valor_numerico, y = Time)) +
geom_point(color='blue') +
geom_smooth(method='lm', color = "red") +
xlab("Valor da causa") +
ylab("Tempo até sentença")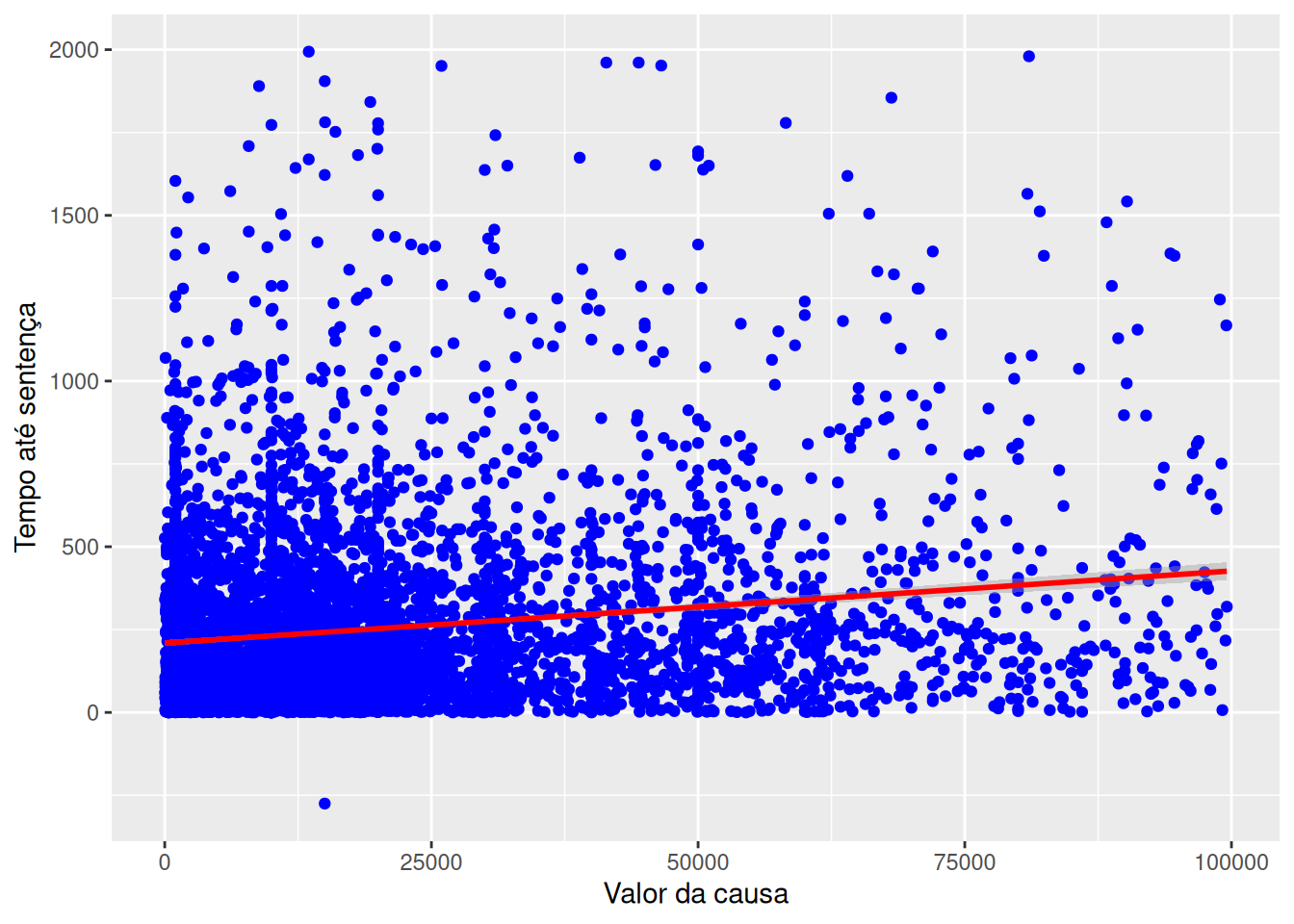
Exercícios
No banco de dados iris, calcule medidas resumo para o comprimento e largura das pétalas e para a largura das sépalas.
Na definição da variância, usamos a média dos desvios quadrado. Esta é uma possível maneira de fazer com que desvios negativos e positivos fossem tratados como iguais. Você consegue pensar em outra forma de eliminar o sinal do desvio que não elevando-o ao quadrado?
Para cada espécie no banco de dados iris, obtenha uma medida de centralidade e uma de variabilidade para o comprimento das sépalas.
O comprimento das sépalas da espécie Iris setosa é consideravelmente menor que o da espécie Iris versicolor que, por sua vez, é menor do que o da espécie Iris virginica. Considere que em um banco de dados temos
Construa um boxplot para os dados: 2.3, 2000, 0.1, 1.5, 0.3, 0.7, 0.2, 1.7 e 1.2.
Parece haver uma relação linear entre o comprimento e largura das sépalas no banco de dados iris?
No banco de dados iris, parece haver diferença entre o comprimento das sépalas entre as 3 espécies observadas?
Uma pesquisadora mediu as alturas de
## [1] 149 163 168 169 172 173 175 180 181Calcule a média e a variância das alturas.
Verifique se há algum outlier neste banco de dados e descreva o significado deste termo.
- Um pesquisador está interessado em estudar como
varia o percentual de aproveitamento do petróleo em
função da temperatura de alimentação do destilador.
Foram consideradas duas diferentes temperaturas
(150 ou 300 graus Celsius) e uma amostra de tamanho
Indique uma medida de centralidade e uma medida de dispersão para cada uma das temperaturas testadas e interprete-as.
Esboce um boxplot para o aproveitamento de petróleo para cada temperatura testada. Interprete os boxplots e compare a diferença entre os aproveitamentos para cada temperatura.
- O boxplot indica a mediana e o intervalo interquartílico de uma variável. Quais são possíveis vantagens destas medidas de centralidade e variabilidade em relação à média e ao desvio padrão?