Propriedades de variáveis aleatórias

Uma forma de descrever a incerteza em relação a uma variável aleatória é por meio de sua função de densidade. Se \(X\) é uma variável aleatória, geralmente designamos a função de densidade de \(X\) por \(f_{X}(x)\). O valor de \(f_{X}(x)\) indica o quão plausível é que a variável aleatória \(X\) assuma o valor \(x\). Por exemplo, a figura abaixo indica uma variável aleatória contínua tal que todos os valores entre 0 e 1 são igualmente plausíveis. Por isso, é comum dizer que esta variável aleatória tem densidade uniforme entre 0 e 1.

library(tidyverse)
ggplot(data.frame(x = c(0, 1)), aes(x)) + 
stat_function(fun = dunif, colour = "red", n = 100)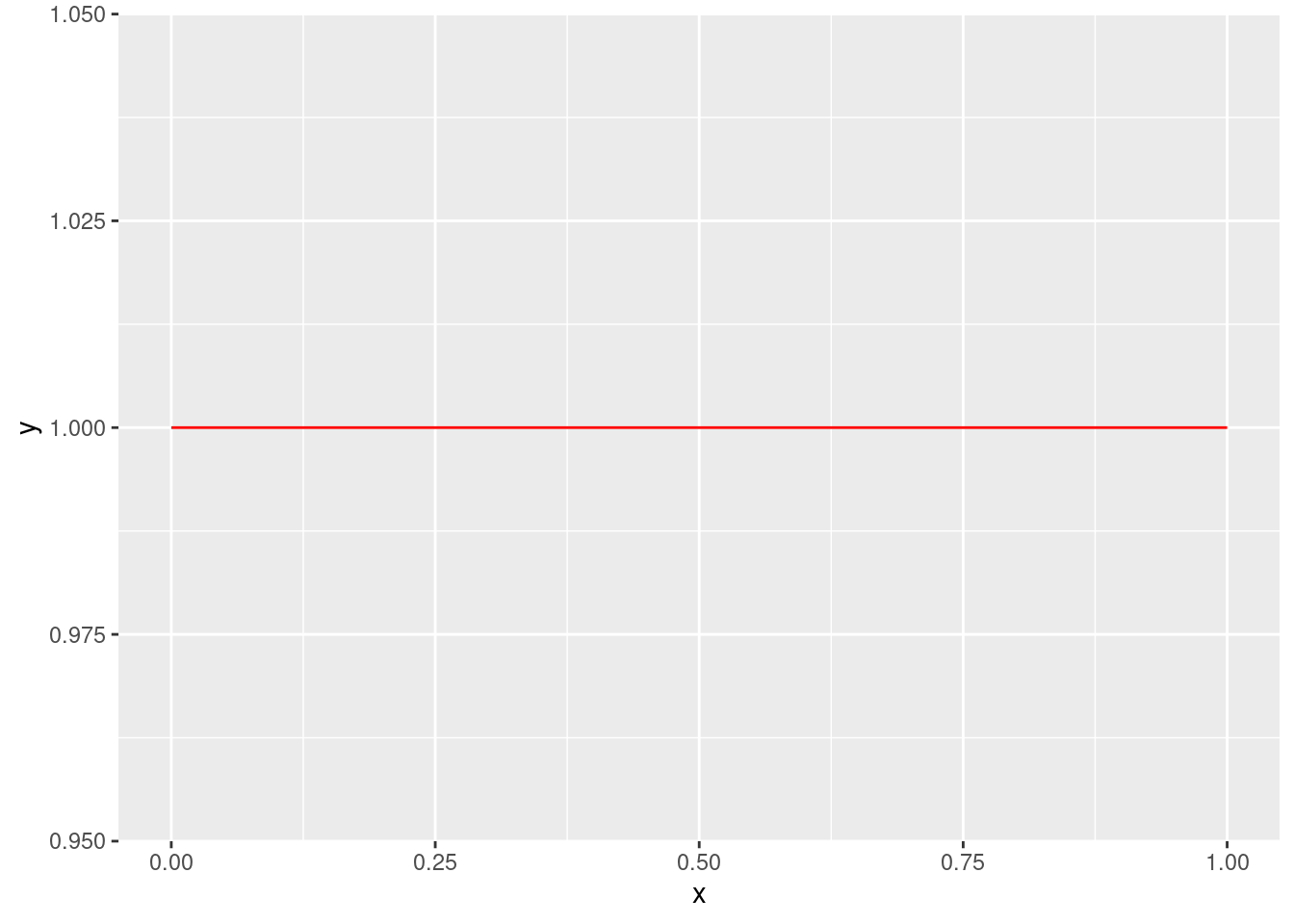

Uma propriedade importante de uma função de densidade é que podemos obter a probabilidade de que \(X\) esteja entre dois valores, \(x_1\) e \(x_2\), calculando a área debaixo da densidade. Note que de corre desta propriedade que a área total debaixo da densidade é \(1\). Por exemplo, a figura abaixo ilustra como obter \(P(0.25 < X < 0.5)\) quando \(X\) tem densidade uniforme entre \(0\) e \(1\). Note que, neste caso, a figura abaixo da curva é um retângulo de base \(0.25\) e altura \(1\) e, portanto, de área \(0.25\). Assim, obtemos que \(P(0.25 < X < 0.5) = 0.25\). Também, a área total debaixo da densidade é dada por um quadrado de lado \(1\), isto é, \(1\). Portanto, como esperávamos, \(P(0 < X < 1) = 1\).

ggplot(data.frame(x = c(0, 1)), aes(x)) + 
stat_function(fun = dunif, colour = "red", n = 100) +
stat_function(fun = dunif, xlim = c(0.25, 0.5), geom = "area", alpha = 0.5)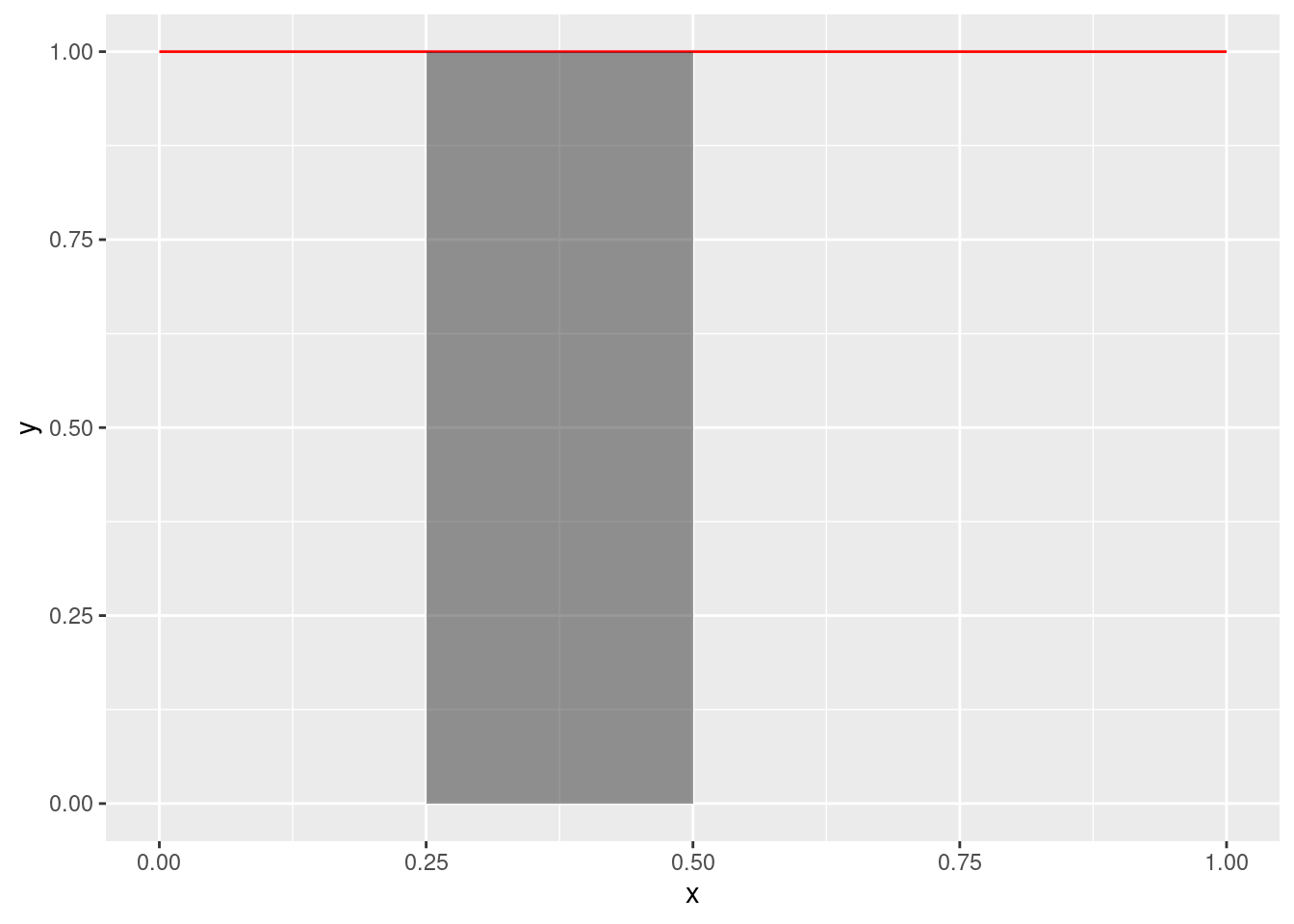 

De forma geral, a área debaixo de uma curva é dada por uma integral. Neste curso não usaremos esta relação, mas é útil saber que, se \(X\) é uma variável contínua, então obtemos que \[P(x_1 \leq X \leq x_2) = \int_{x_1}^{x_2} f_{X}(x)dx\]

Também note que a área entre \(x_1\) e \(x_2\) pode ser descrita como a área à esquerda de \(x_2\) subtraída da área à esquerda de \(x_1\). Assim, se \(X\) é uma variável contínua, também vale a seguinte relação \[P(x_1 \leq X \leq x_2) = P(X \leq x_2) - P(X \leq x_1)\]

A função de densidade descreve toda a incerteza sobre uma variável aleatória. Contudo, pode ser difícil descrever e analisar uma função. Assim, é comum que certos aspectos de uma variável aleatória sejam resumidos em números. A seguir, estudamos algumas destas medidas resumo.

• Esperança (média populacional): A esperança de uma varíavel aleatória, \(X\) é denotada por \(E[X]\) e descreve uma medida de centralidade desta. Se imaginarmos que, para cada possível valor, \(x\), existe um peso de \(f_{X}(x)\) na posição \(x\), então \(E[X]\) descreve o centro de massa desse sistema. Também, a média amostral e a esperança resumem a mesma característica. Enquanto que a primeira descreve a centralidade para uma variável em um banco de dados, uma variável aleatória já observada, a segunda descreve a centralidade para uma variável aleatória, isto é, descreve a incerteza sobre uma observação antes que esta ocorra. De forma técnica, a esperança de uma variável aleatória contínua é calculada da seguinte forma: \[E[X] = \int_{-\infty}^{\infty}{x f_{X}(x)dx}\]

• Variância (populacional): A variância de uma variável aleatória, \(X\), é denotada por \(V[X]\) e indica um resumo da variabilidade desta. Assim como a variância amostral descreve a variabilidade de uma variável em um banco de dados (já observado), a variância populacional descreve a variabilidade de uma variável aleatória (ainda não observada). De forma técnica, a variância de uma variável aleatória contínua é calculada da seguinte forma: \[V[X] = \int_{-\infty}^{\infty}{(x-E[X])^2 f_{X}(x)}dx\] Semelhantemente ao caso da variância amostral, a variância populacional não é medida na mesma escala da variável aleatória que ela representa. Para obter esta escala, é comum tomar a raiz quadrada da variância populacional. Esta medida é chamada de desvio padrão (populacional). Também é comum designarmos a variância de \(X\) por \(\sigma^2_X\). Esta notação é conveniente pois permite designarmos o desvio padrão de \(X\) por \(\sigma_X\).

A seguir, estudaremos algumas funções de densidade essenciais para este curso.

Distribuição normal

Uma das distribuições mais usadas é a Normal. Formalmente, dizemos que \(X\) tem distribuição normal com média \(\mu\) e variância \(\sigma^2\) se \(X\) pode assumir qualquer número real e sua densidade, \(f_{X}(x)\), tem a forma \[ f_{X}(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \] Como diremos muitas vezes neste curso que “\(X\) tem distribuição Normal com média \(\mu\) e variância \(\sigma^2\)”, abreviaremos esta expressão por \(X \sim N(\mu,\sigma^2)\). Se \(X \sim N(\mu,\sigma^2)\), então obtem-se que \(E[X] = \mu\) e \(Var[X] = \sigma^2\). A figura abaixo exibe a densidade da \(N(0,1)\), também conhecida por “normal padrão”.

ggplot(data.frame(x = c(-3, 3)), aes(x)) + 
stat_function(fun = dnorm, colour="red", n = 100)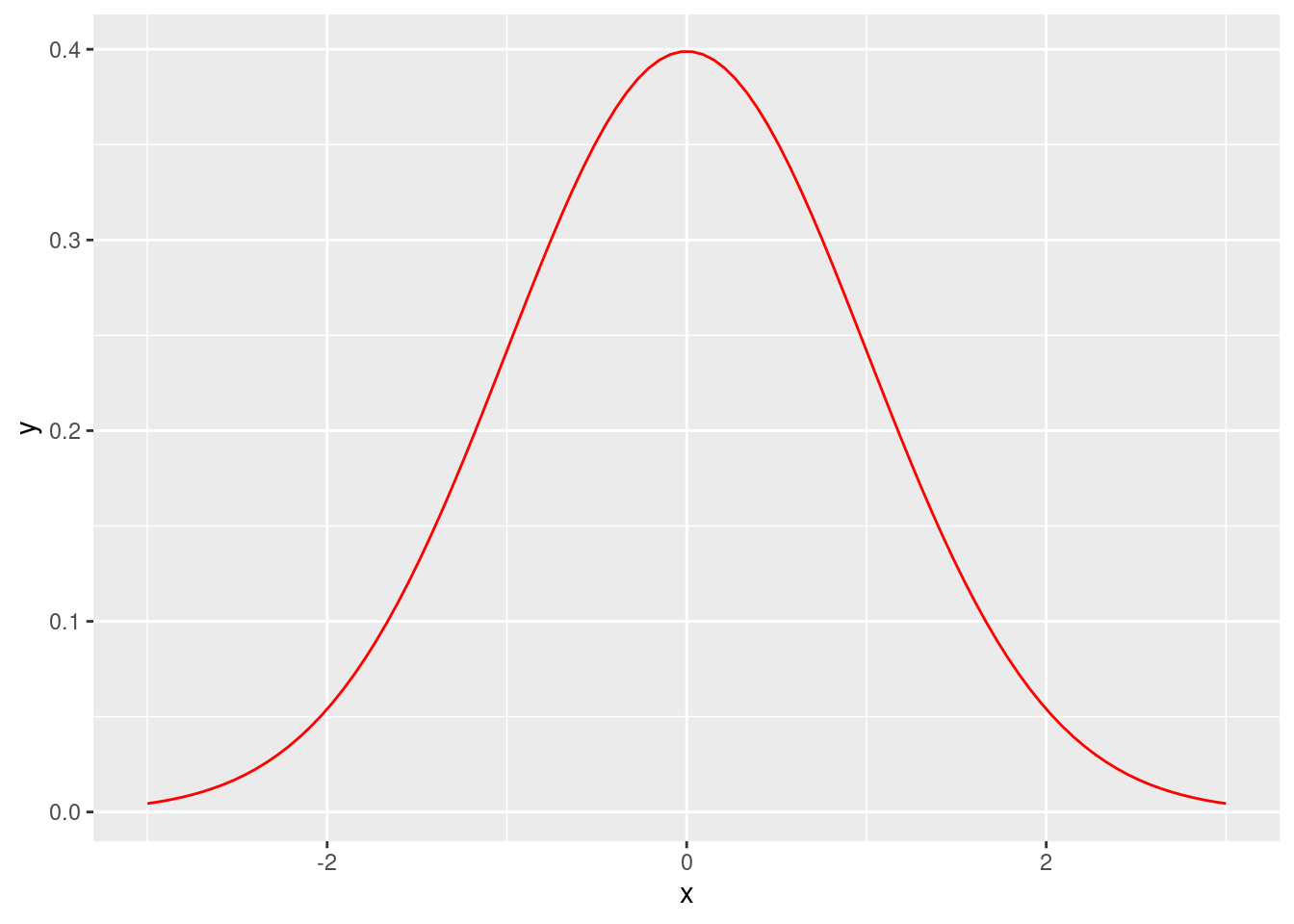 

Note que a densidade tem um formato de sino com simetria ao redor do \(0\). Decorre que a normal padrão tem média \(0\). A densidade de uma normal com média \(\mu\) e variância \(1\) terá o mesmo formato, só que transladado por \(\mu\). Este fato é ilustrado na figura a seguir, em que as curvas azul e verdem indicam, respectivamente, as densidades da \(N(-1,1)\) e da \(N(1,1)\).

ggplot(data.frame(x = c(-4,4)), aes(x)) + 
stat_function(fun = dnorm, colour = "red", n = 100) +
stat_function(fun = function(x) dnorm(x, mean = -1), 
              colour = "blue", n = 100) +
stat_function(fun = function(x) dnorm(x, mean = 1), 
              colour = "green", n = 100) +
ylab("densidade")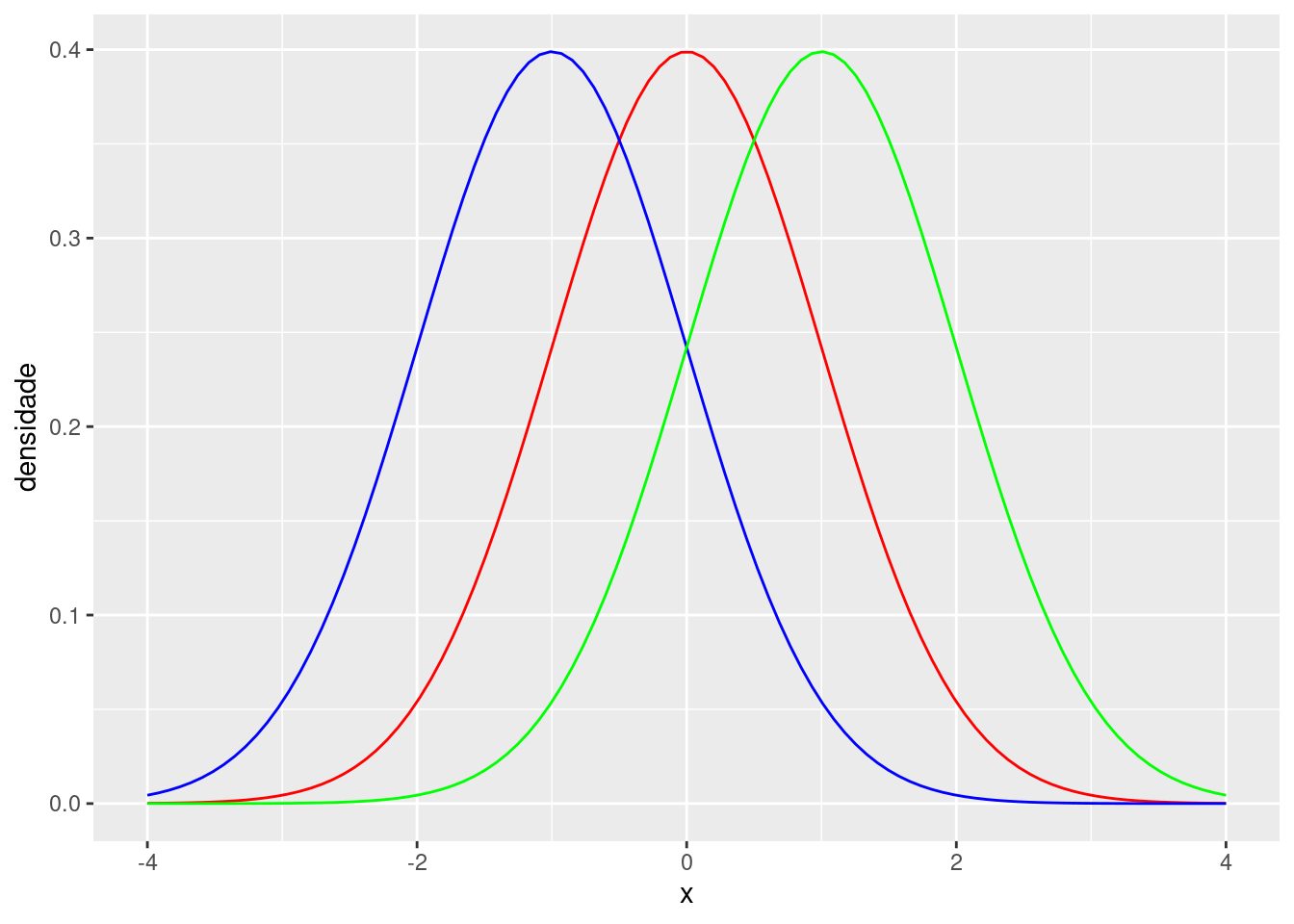

Semelhantemente, a figura abaixo apresenta nas curvas verde, vermelha e azul, respectivamente, as distribuições \(N(0, 0.25)\), \(N(0, 1)\) e \(N(0, 4)\). Note que a variância, \(\sigma^2\), altera a escala da densidade da normal. Quanto menor o valor de \(\sigma^2\), mais a densidade está concentrada ao redor da média.

ggplot(data.frame(x = c(-6,6)), aes(x)) + 
stat_function(fun = dnorm, colour = "red", n = 100) +
stat_function(fun = function(x) dnorm(x, sd = 2), 
              colour = "blue", n = 100) +
stat_function(fun = function(x) dnorm(x, sd = 0.5), 
              colour = "green", n = 100) +
ylab("densidade")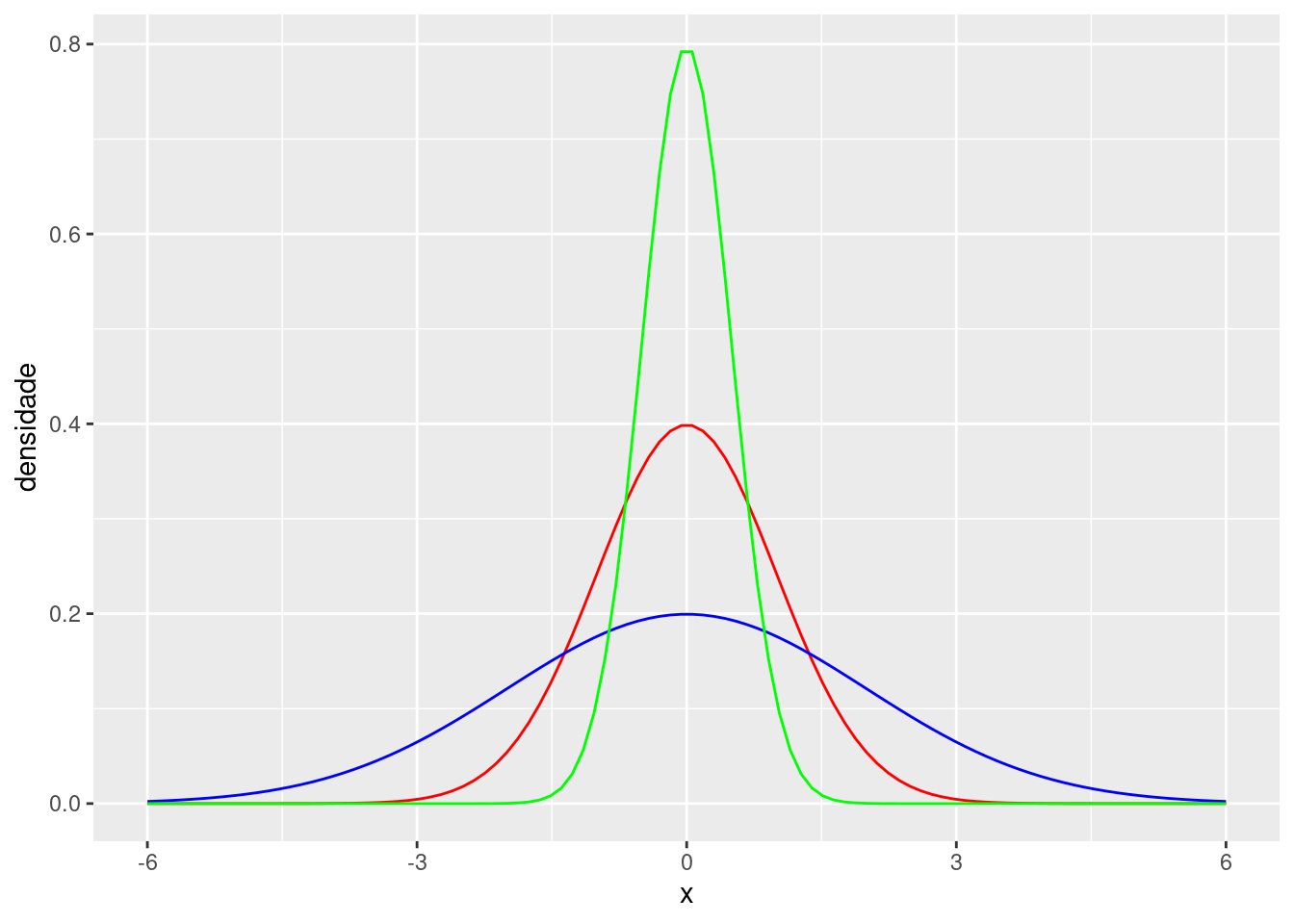

Uma relação útil é que aproximadamente 95% da densidade de uma \(N(\mu,\sigma^2)\) está concentrada entre \(\mu-2\sigma\) e \(\mu+2\sigma\). Na figura acima, temos que \(\mu=0\). Assim, aproximadamente 95% da área das curvas verde, vermelha e azul está concentrada, respectivamente, em \([-1,1]\), \([-2,2]\) e \([-4,4]\). De forma mais formal, se \(X \sim N(\mu,\sigma^2)\) e \(\approx\) significa aproximadamente, então \[ P(\mu-2\sigma \leq X \leq \mu+2\sigma) \approx 0.95 \]

Se \(X \sim N(\mu,\sigma^2)\), não é possível descrever \(P(X \leq x)\) de forma analítica. Contudo, é possível obter uma aproximação analítica para esta quantidade no R usando a função pnorm. Por exemplo, o código abaixo calcula \(P(X \leq 4)\) para uma \(N(2,9)\).

pnorm(4, mean = 2, sd = 3)

## [1] 0.7475075

Também a probabilidade de que uma \(N(2,9)\) esteja entre \(1\) e \(4\) é obtida da seguinte forma:

pnorm(4, mean = 2, sd = 3) - pnorm(1, mean = 2, sd = 3)

## [1] 0.3780661

É possível transformar qualquer distribuição normal em uma normal padrão por meio de transformações lineares. Especificamente, se \(X \sim N(\mu,\sigma^2)\), então \(\frac{X-\mu}{\sigma} \sim N(0,1)\). Por isso, podemos imaginar que obtemos uma \(N(\mu,\sigma^2)\), ao multiplicar uma normal padrão por \(\sigma\) e somar \(\mu\) ao resultado. O processo de calcular \(\frac{X-\mu}{\sigma}\) é frequentemente chamado de padronização.

medias = rep(NA, 1000)
for(ii in 1:1000) 
{
  medias[ii] = mean(runif(100, 0, 1))
}
ggplot(aes(x = medias), data = data.frame(medias)) +
geom_histogram(aes(y = ..density..)) +
geom_density(colour="red")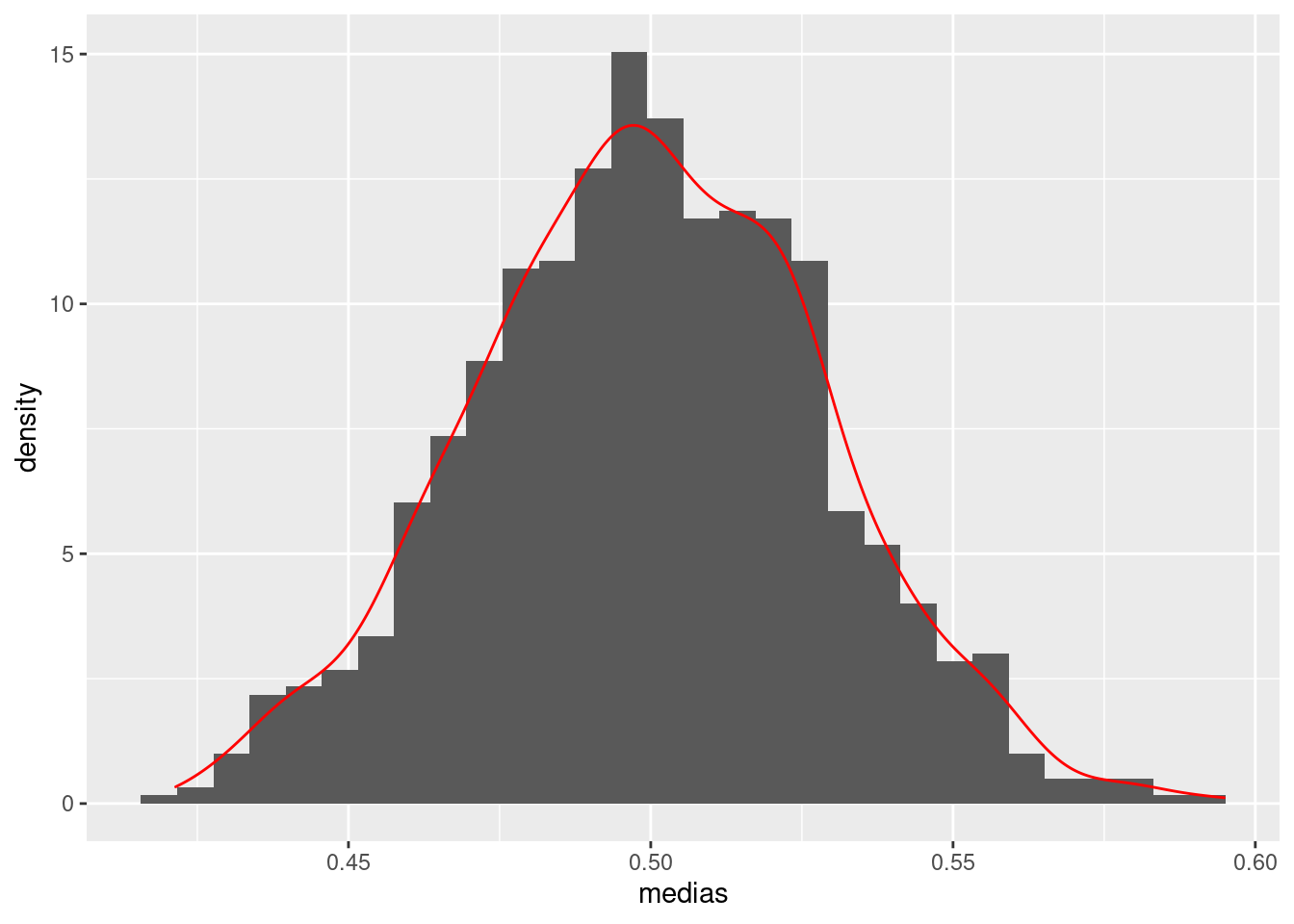

Distribuição chi-quadrado

• Se \(X\) tem distribuição chi-quadrado com \(n\) graus de liberdade, escrevemos \(X \sim \chi^2_n\). Neste caso, \[f_{X}(x) = \frac{x^{0.5n-1}\exp(-0.5x)}{2^{0.5n}\Gamma(0.5n)},\] \(E[X]=n\) e \(V[X]=2n\).

• Se \(X \sim N(0,1)\), então \(X^2 \sim \chi^2_1\).

• Se \(X_1, \ldots, X_n\) são variáveis independentes e cada qual tem distribuição \(\chi^2_1\), então \(\sum_{i=1}^n X_i \sim \chi^2_n\).

• Se \(X_1, \ldots, X_n\) são variáveis independentes e tais que \(X_{i} \sim N(\mu, \sigma^2)\), então \(\frac{\sum_{i1=}^{n}(X_i-\bar{X})^2}{\sigma^2} \sim \chi^2_{n-1}\), ou seja, \(\frac{S^2}{\sigma^2} \sim \chi^2_{n-1}\).

• No R, podemos obter a densidade e \(P(X \leq x)\) para a chi-quadrado por meio dos comandos dchisq e pchisq.

Distribui??o T de Student

• Designamos a distribui??o \(T\) de Student com \(n\) graus de liberdade por \(T_{n}\).

• Se \(Z \sim N(0,1)\) e \(S^2 \sim \chi^2_n\) s?o vari?veis independentes, ent?o \(\frac{Z}{\sqrt{\frac{S^2}{n}}} \sim T_{n}\).

• No R, podemos obter a densidade e \(P(X \leq x)\) para a T de Student por meio dos comandos dt e pt.

Distribuição F de Snedcor

• Se \(X\) tem distribuição \(F\) com parâmetros \(d_1\) e \(d_2\), então escrevemos \(X \sim F_{d_1,d_2}\).

• \(X_1 \sim \chi^2_{d_1}\), \(X_2 \sim \chi^2_{d_2}\) e \(X_1\) e \(X_2\) são independentes, então

\[ \frac{\frac{X_1}{d_1}}{\frac{X_2}{d_2}} \sim F_{d_1,d_2} \]

• No R, podemos obter a densidade e \(P(X \leq x)\) para a distribuição F por meio dos comandos df e pf.

Exercícios

1. Se \(X\) tem densidade entre uniforme entre \(0\) e \(1\) e \(0 \leq x_1, x_2 \leq 1\), calcule \(P(x_1 \leq X \leq x_2)\).

2. Se \(X\) tem densidade uniforme entre \(1\) e \(3\), qual é o valor da densidade de \(X\) neste intervalo?

3. Calcule a esperança e a variância de uma variável aleatória com distribuição uniforme entre \(0\) e \(1\).

4. Ache um intervalo tal que uma \(N(4,9)\) e steja dentro deste com probabilidade aproximadamente \(95\%\).

5. Se \(X \sim N(4,9)\), utilize o R para calcular \(P(-1 \leq X \leq 1)\).

6. Se \(X \sim N(10, 100)\), indique uma transformação linear de \(X\) que tem distribuição normal padrão.

7. Se \(X_1, \ldots, X_n\) são variáveis independentes de mesma distribuição e tais que \(E[X_i] = 9\) e \(V[X_i] = 16\), indique valores para \(a\) e \(b\) tal que \(P(a \leq \bar{X} \leq b) \approx 95\%\).

8. Um pesquisador utilizou uma mesma medida resumo em diversas variáveis de seu banco de dados. Para visualizar estas medidas, construiu um histograma delas. Este histograma se encontra abaixo. Com base no histograma, argumente se a medida resumo poderia ou não ser a média amostral.

Referências